Tabellen: hoe ga je ermee om?
Tabellen. Je zag ze al op de basisschool. Toen ging het nog om een paar simpele getallen of misschien was het gewoon een potje boter-kaas-en-eieren. Ook na de basisschool krijg je nog steeds met tabellen te maken. En sommige tabellen kunnen best complex zijn. Hoe kun je tabellen het beste lezen? En hoe haal je specifieke informatie uit een tabel? In dit artikel kun je alles lezen over het omgaan met tabellen.

Wat is een tabel?

Tabellen zijn lijsten met getallen die de bepaalde resultaten weergeven in vakjes. Tabellen worden vaak gebruikt om specifieke data weer te geven. Het programma Excel wordt bijvoorbeeld vaak gebruikt om tabellen mee te maken.
Een tabel bestaat horizontaal uit de rijen en verticaal uit de kolommen. De structuur van een tabel ziet er dus als volgt uit:
| Kolom 1 | Kolom 2 | Kolom 3 | |
|---|---|---|---|
|
Rij 1 |
|
|
|
|
Rij 2 |
|
|
|
|
Rij 3 |
|
|
|
Voorbeelden

Het is belangrijk te weten hoe je met tabellen omgaat en hoe je specifieke informatie uit een tabel kunt halen. Dit gaan we laten zien aan de hand van een paar voorbeelden.
Voorbeeld 1
In onderstaande tabel zie je de woningsituatie in een land in de afgelopen eeuw.
| Jaar | Aantal woningen (x1000) | Aantal kamers (x1000) | Aantal inwoners (x1000) |
|---|---|---|---|
|
1905 |
1426 |
3871 |
6201 |
|
1942 |
1789 |
8001 |
7579 |
|
1965 |
2112 |
10125 |
9201 |
|
1997 |
3901 |
20181 |
12802 |
Vraag 1.1: is het aantal inwoners per woning sinds 1905 toe- of afgenomen?
Antwoord
- In 1905 waren er 6.201.000 inwoners en 1.426.000 woningen.
- 6.201.000 / 1.426.000 = 4,349.
- Dat betekent dus ongeveer 4 inwoners per woning.
- In 1997 waren er 12.802.000 inwoners en 3.901.000 woningen.
- 12.802.000 / 3.901.000 = 3,282.
- Dat betekent dus ongeveer 3 inwoners per woning.
Het aantal inwoners per woning sinds 1905 is dus afgenomen.
Vraag 1.2: hoe heeft het aantal personen per kamer zich in de vorige eeuw ontwikkeld?
Antwoord
- In 1905 waren er 3.871.000 kamers en 6.201.000 inwoners.
- 6.201.000 / 3.871.000 = 1,602 inwoners per kamer.
- Dit betekent dat er in 1905 ongeveer 1,602 inwoners per kamer waren.
- In 1942 zijn dat er 7.579.000 / 8.001.000 = 0,947.
- Dat is dus ongeveer iets minder dan in 1905.
- In 1965 zijn dat er 9.201.000 / 10.125.000 = 0,910.
Conclusie: in de loop der jaren neemt het aantal personen per kamer steeds meer af.
Voorbeeld 2
In onderstaande tabel zie je de sterfgevallen als gevolg van een virus. Ook is er onderscheid gemaakt in mannelijke en vrouwelijke slachtoffers.
| Jaar | Totaal | Aantal mannen | Aantal vrouwen |
|---|---|---|---|
|
2012 |
135.987 |
66.021 |
70.021 |
|
2013 |
136.001 |
65.242 |
70.382 |
|
2014 |
141.013 |
68.020 |
72.982 |
|
2015 |
141.223 |
68.040 |
72.654 |
|
2016 |
139.226 |
67.025 |
72.058 |
|
2017 |
147.139 |
71.002 |
76.085 |
|
2018 |
149.002 |
72.181 |
76.819 |
|
2019 |
150.218 |
72.592 |
77.448 |
Vraag 2.1: welk percentage van het totaal aantal sterfgevallen door het virus was man in het jaar 2012?
Antwoord
- (66.021 / 135.987) × 100% = 48,55%.
Vraag 2.2: is het percentage van mannelijke sterfgevallen door het virus afgenomen of toegenomen in het jaar 2016 ten opzichte van 2012?
Antwoord
- (67.025 / 139.226) × 100% = 48,14%.
In 2012 was het percentage 48,55%, terwijl dit in 2016 48,14%. Het percentage van mannelijke sterfgevallen is in die periode dus afgenomen.
Vraag 2.3: wat was de gemiddelde groei of afname van het aantal vrouwelijke sterfgevallen door het virus in de fase van 2016 tot 2019?
Antwoord
- Groei van 2016 naar 2017: 76.085 – 72.058 = 4.027.
- Groei van 2017 naar 2018: 76.819 – 76.085 = 734.
- Groei van 2018 naar 2019: 77.448 – 76.819 = 629.
Dus de gemiddelde groei tussen 2016 en 2019 = (4.027 + 734 + 629) / 3 = 1.796,67.
Of:
De gemiddelde groei tussen 2016 en 2019 = (77.448 - 72.058) / 3 = 1796,67.
Vraag 2.4: zijn er in totaal meer mannelijke of vrouwelijke sterfgevallen door het virus in de fase van 2012 tot en met 2019?
Antwoord
In de tabel is te zien dat er meer vrouwelijke sterfgevallen zijn door het virus dan mannelijke sterfgevallen. Dit kun je achterhalen door simpelweg alle mannelijke doden bij elkaar op te tellen (derde kolom) en alle vrouwelijke doden bij elkaar op te tellen (vierde kolom).
Voorbeeld 3
De politie heeft in 2020 veel vervalste eurobiljetten in beslag genomen. In onderstaande tabel kun je aflezen hoe de procentuele verdeling is tussen de verschillende in beslag genomen biljetten, zowel in Nederland als in België.
| €5 | €10 | €20 | €50 | €100 | €200 | €500 | |
|---|---|---|---|---|---|---|---|
|
Nederland |
1% |
1,5% |
18% |
48% |
11% |
2% |
2,5% |
|
België |
0,8% |
3,5% |
47% |
36% |
12,5% |
2,3% |
0,5% |
Vraag 3.1: in 2020 zijn er in Nederland 34.000 valse eurobiljetten door de politie in beslag genomen. Bereken met behulp van de tabel hoeveel valse eurobiljetten van €50 er in 2020 in Nederland in beslag zijn genomen. Laat zien hoe je het berekend hebt.
Antwoord
- 0,48 × 34.000 = 16.320.
Dus in 2020 is er een totaal van 16.320 biljetten van 50 euro in beslag genomen. Let vooral goed op dat je kijkt naar de rij van Nederland en niet naar de rij van België.
Verbanden herkennen in tabellen

Uit een tabel kun je ook verbanden herkennen. Hieronder laten we je een voorbeeld zien van een tabel die een lineair verband aangeeft en een die een exponentieel verband aangeeft.
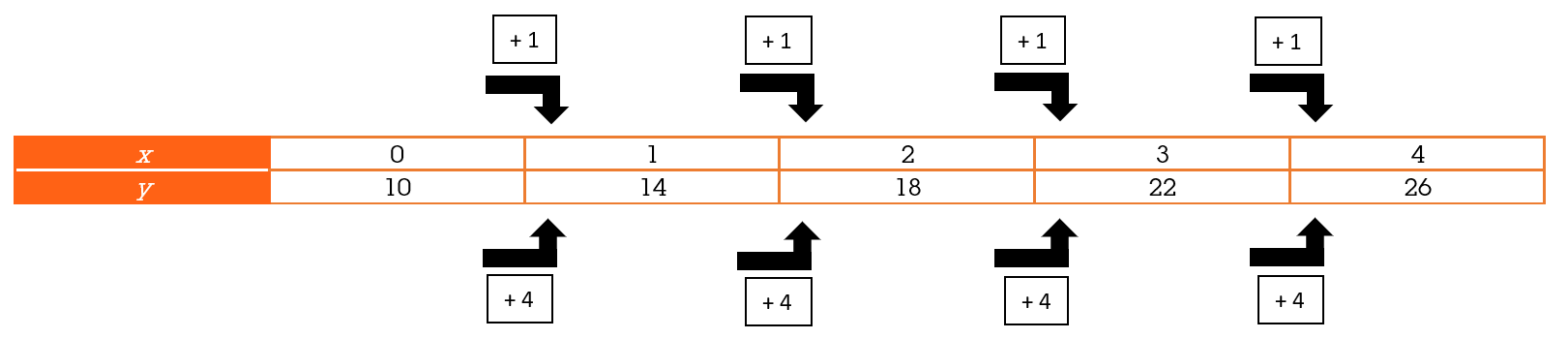
Tabel met een lineair verband
In onderstaande tabel is een lineair verband terug te zien, namelijk y = 10 + 4x.
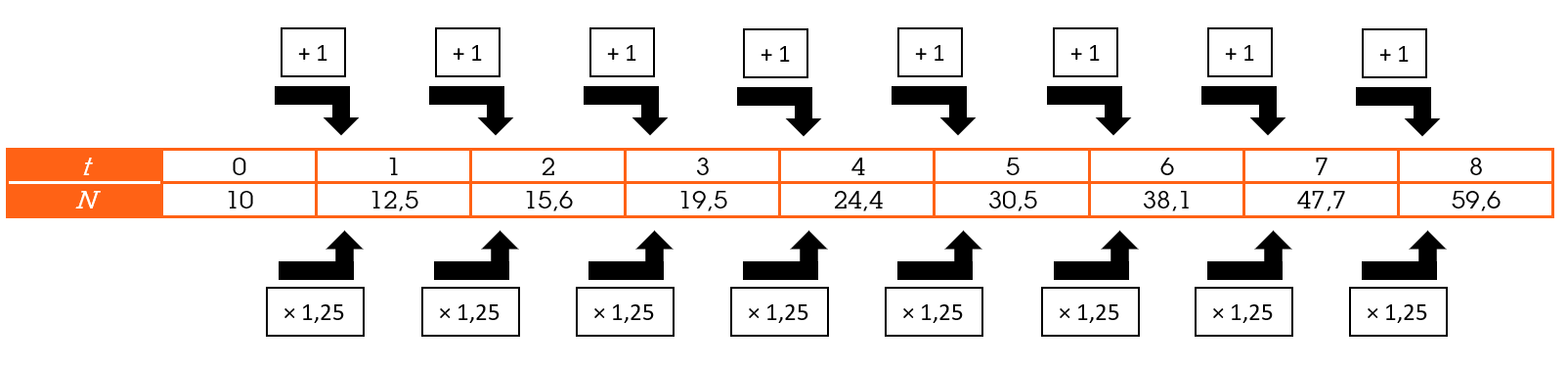
Tabel met een exponentieel verband
In onderstaande tabel is een exponentieel verband terug te zien, namelijk N = 10 × 1,25t.
Als je de waarde van N deelt door de voorgaande waarde van N, kom je uit op 1,25 (bijvoorbeeld 19,5 / 15,6 = 1,25). Dit is de groeifactor. Zo zie je dat je uit een tabel een formule kunt afleiden.
Video
Wil je de uitleg over het aflezen van informatie uit een tabel het liefst ook nog even terugzien op video? Kijk dan onderstaande video van Math with Menno.