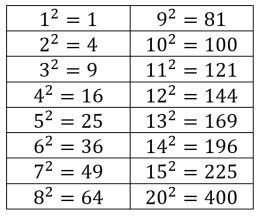Hoe werkt de stelling van Pythagoras?

Met behulp van de stelling van Pythagoras kan je de lengte van een zijde in een rechthoekige driehoek berekenen. Deze stelling, a² + b² = c², is één van de bekendste stellingen in de wiskunde.

Basiskennis om met de stelling van Pythagoras te kunnen werken

Om met de stelling van Pythagoras te kunnen werken, heb je de volgende basiskennis nodig.

Kwadraten

Het kwadraat nemen van een getal betekent eigenlijk dat je het getal met zichzelf vermenigvuldigt. Zo is 9² = 81, want 9² = 9 × 9 = 81. Het is verstandig om minimaal de kwadraten van 1 tot en met 15 uit je hoofd te leren. Door het kwadraat te nemen van de zijde van een vierkant, bereken je de oppervlakte van het vierkant.

Wortels

Een wortel is eigenlijk het omgedraaide van een kwadraat. 11² = 121, dus √121 = 11. Wanneer je de kwadraten goed kent, zou je de wortels moeten herkennen.

Rechthoekige driehoek

Een rechthoekige driehoek is een driehoek waarvan één van de hoeken 90° is.

Rechthoekszijde

Een rechthoekszijde is de zijde die de rechte hoek raakt. Een rechthoekige driehoek heeft 2 rechthoekszijden. Dit zijn de benen van de rechte hoek.

De stelling van Pythagoras

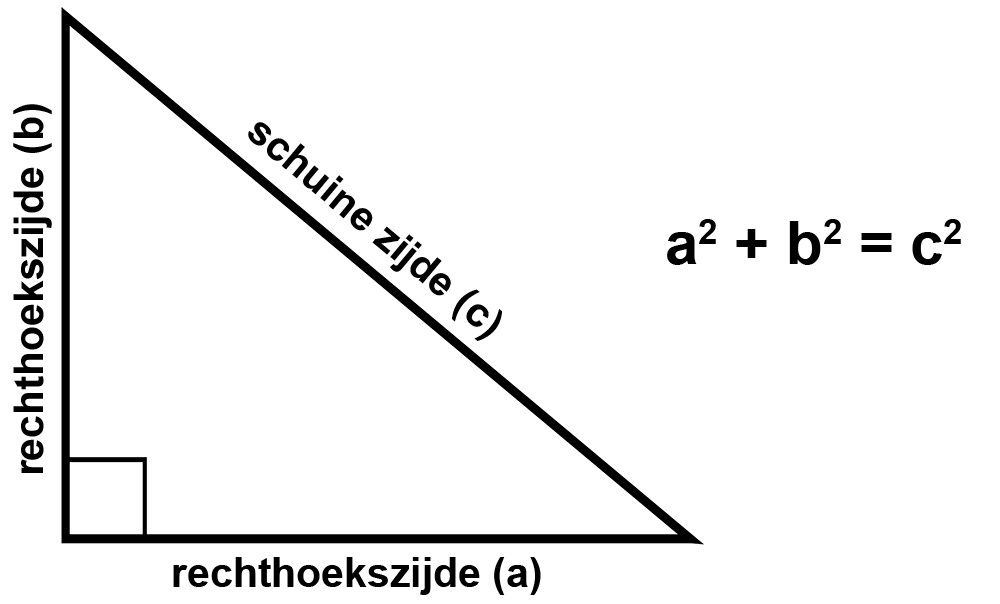
Een rechthoekige driehoek heeft 3 zijdes: 2 rechthoekszijden en een schuine zijde. De schuine zijde wordt ook wel eens de langste zijde, of de hypotenusa genoemd. Bij de stelling van Pythagoras kan je de schuine zijde berekenen wanneer je de 2 rechthoekszijden weet. De stelling wordt vaak aangegeven als a² + b² = c². Hierin zijn a en b de rechthoekszijden en c de schuine zijde.

De langste zijde berekenen met de stelling van Pythagoras

Het handigste is om een tabel te maken om de stelling van Pythagoras uit te rekenen.

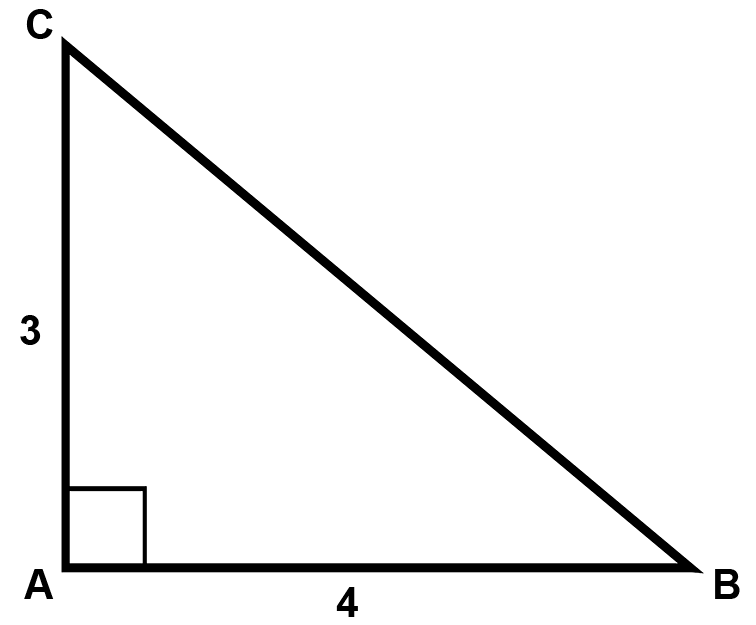
Voorbeeld: gegeven is rechthoekige driehoek ABC met rechthoekszijde AB, 4 cm, en rechthoekszijde AC, 3 cm, en de schuine zijde BC.

Je kunt dan een tabel maken:

Zoals je ziet zijn de kwadraten van de twee rechthoekszijden bij elkaar opgeteld 25. De wortel van 25 is 5. Daarom is zijde BC 5 cm lang.

Een andere manier om BC te berekenen is via een formule:

AB² + AC² = BC²
4² + 3² = BC²
16 + 9 = BC²
BC² = 16 + 9
BC² = 25
BC = √25 = 5

Een rechthoekszijde berekenen met de stelling van Pythagoras

Het kan ook voorkomen dat je de schuine zijde en één rechthoekszijde gegeven krijgt. Hier moet je dan de overige rechthoekszijde uitrekenen. Voorbeeld:

Zoals je ziet hebben we hier een rechthoekige driehoek met een schuine zijde van 13 en een rechthoekszijde van 12. De vraag is hier om AC te berekenen.

Volgens Pythagoras geldt de formule: AB² + AC² = BC². We weten nu de waarde van BC en de waarde van AB. AC zal berekend moeten worden.

Via de tabel

Je ziet nu dat 144 + ? = 169. Het vraagteken moet dan gelijk zijn aan 169 –144 = 25.

Aangezien je weet dat het kwadraat van AC nu gelijk is aan 25, kun je AC berekenen door de wortel te nemen van 25. Hierdoor krijg je als antwoord AC = 5 cm.

Via de formule

AB² + AC² = BC²
12² + AC² = 13²
144 + AC² = 169
AC² = 169 – 144
AC² = 25
AC = √25 = 5

Rechthoekigheid van een driehoek controleren met de stelling van Pythagoras

Wanneer je een rechthoekige driehoek hebt, klopt de stelling van Pythagoras altijd. Je zou dus kunnen controleren of een driehoek rechthoekig is, door de stelling van Pythagoras te gebruiken.

Voorbeeld:

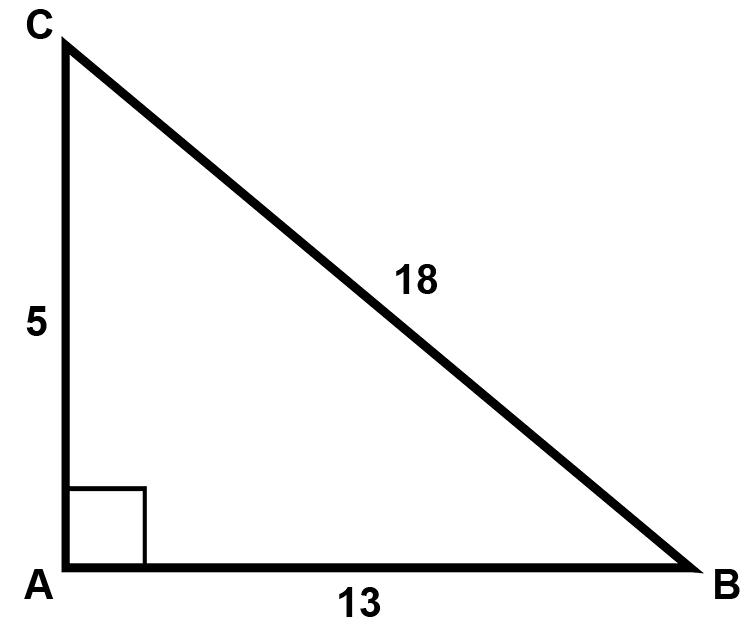
Gegeven de driehoek ABC. Is deze driehoek rechthoekig?

Als de driehoek rechthoekig is, zou de stelling van Pythagoras moeten kloppen.

AB² + AC² = BC²
13² + 5² =? 18²
169 + 25 ≠ 324

Aangezien de stelling van Pythagoras niet klopt bij deze driehoek, mag je zeggen dat de driehoek ABC niet rechthoekig is.

Video

Wil je nog een keer een samenvatting op video zien van de stelling van Pythagoras? Kijk dan onderstaande video van WiskundeAcademie.