Wat is het verschil tussen sinus, cosinus en tangens?

In de wiskunde ben je ongetwijfeld wel eens de begrippen sinus, cosinus en tangens tegengekomen. Maar waar gebruik je ze precies voor? En wat betekent SOS CAS TOA nu eigenlijk? In dit artikel lees je alles over sinus, cosinus en tangens.

Basiskennis om te werken met sinus cosinus en tangens

Voordat je kunt werken met sinus, cosinus en tangens, moet je weten wat een rechthoekige driehoek is. Een rechthoekige driehoek is een driehoek waarvan één van de hoeken 90° is. Ook moet je weten wat een rechthoekszijde is. Dit is de zijde die de rechte hoek raakt. Een rechthoekige driehoek heeft twee rechthoekszijden. Dit zijn de benen van de rechte hoek.

De rechthoekige driehoek

Je kunt alleen gebruik maken van de sinus, cosinus en tangens als je een rechthoekige driehoek hebt. Bij een andere driehoek kan je hier dus géén gebruik van maken.

In de rechthoekige driehoek moet je kunnen aangeven wat de zijdes zijn vanuit een hoekpunt. De keuzes hierin zijn:

• Schuine zijde
• Aanliggende rechthoekszijde
• Overstaande rechthoekszijde

Voorbeeld:

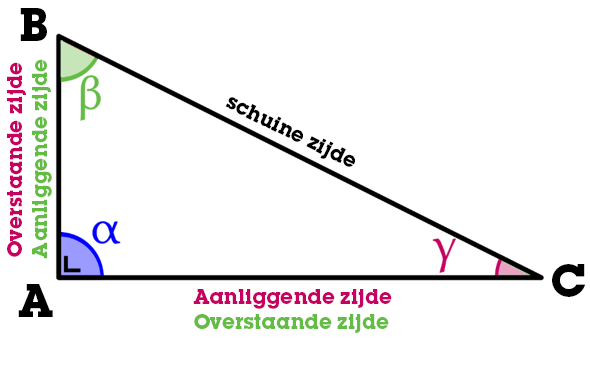
Hier zie je dat vanuit hoekpunt B (β), zijde AC de overstaande zijde is. Deze zijde ‘raakt’ hoekpunt B ook niet, waardoor deze de overstaande is. Zijde AB is vanuit hoekpunt B de aanliggende zijde. Deze ligt tegen hoekpunt B aan.

Voor hoekpunt C (γ) geldt dat AB de overstaande zijde is, want AB raakt hoekpunt C niet. AC is dan de aanliggende zijde, want deze zijde raakt hoekpunt C aan. 

De schuine zijde is altijd de zijde tegenover de rechte hoek.

Het gebruik van sinus, cosinus en tangens

De sinus(sin), cosinus(cos) en tangens(tan) geven een verhouding tussen twee zijdes in een rechthoekige driehoek. Hierbij horen de volgende formules die je uit je hoofd moet leren.

Vanuit hoek A:

Vanuit hoek C:

Een handig ezelsbruggetje hiervoor is SOS CAS TOA

Het berekenen van een hoek

De sinus, cosinus en tangens geven de verhouding van zijdes in een rechthoekige driehoek aan. Wanneer je van een rechthoekige driehoek de lengtes van de zijdes weet, kan je de hoek berekenen door middel van de inverse van de sinus, cosinus of tangens (sin^–1, cos^–1, tan^–1). Deze kan je op je rekenmachine vinden door eerst de shift in te drukken en vervolgens sin, cos of tan.

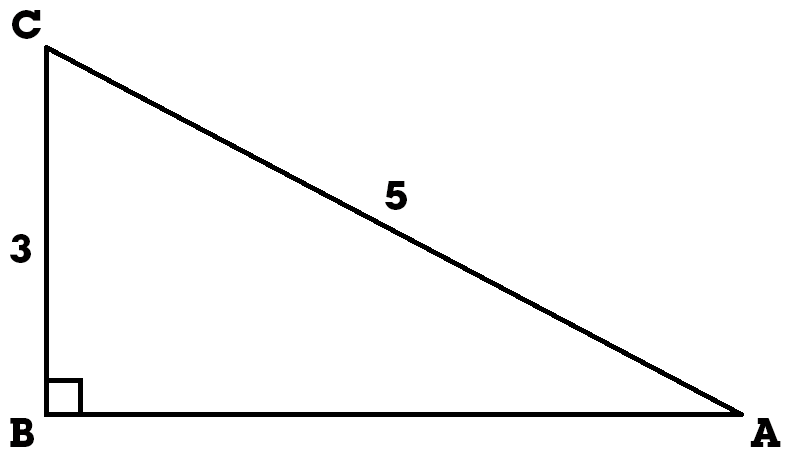
Een voorbeeld:

In de driehoek hierboven zijn 2 zijdes gegeven. We willen de grootte van hoek A berekenen.

Vanuit hoek A weten we de overstaande rechthoekszijde (BC) en de schuine zijde (AC). Dit zorgt ervoor dat we de sinus moeten gebruiken (SOS).

We kunnen hier ook de grootte van hoek C berekenen. Hier weten we namelijk de aanliggende rechthoekszijde (BC) en de schuine zijde (AC) van. Bij de aanliggendeen schuine zijde gebruiken we de cosinus (CAS).

Hier kan je dus ook zien dat het een groot verschil is of je de sinus of de cosinus gebruikt. Daarom is het belangrijk dat je goed kijkt welke je nodig hebt.

Het berekenen van een zijde

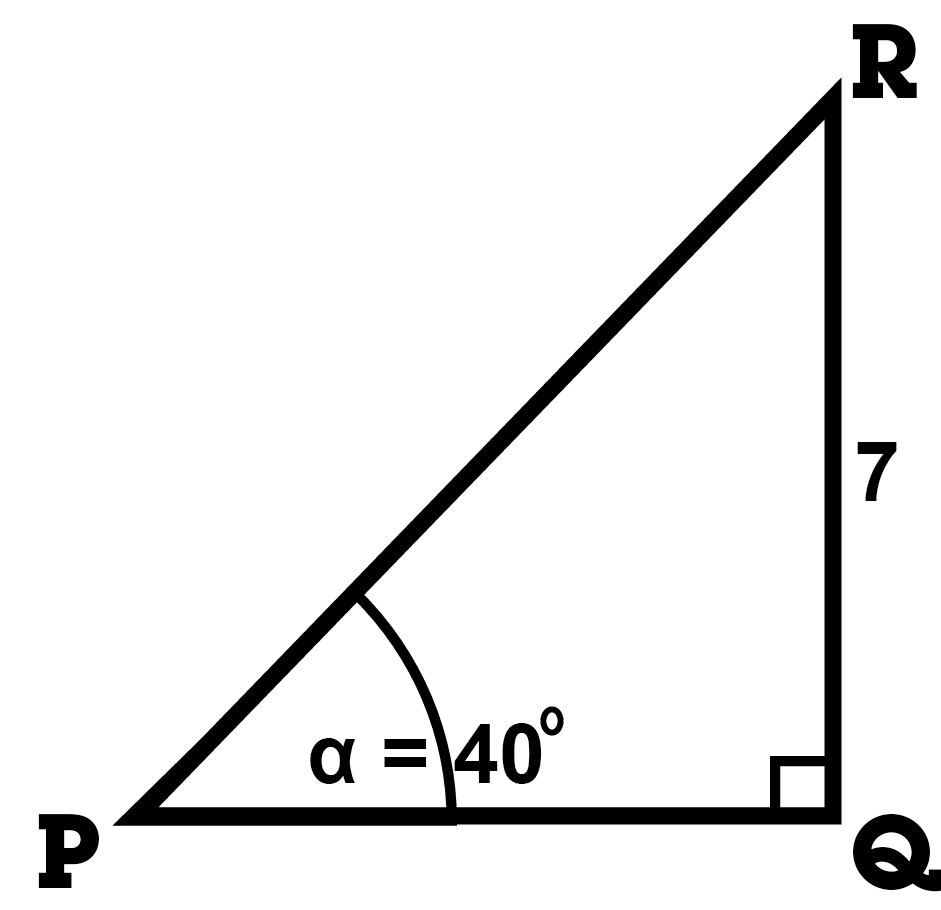
Wanneer je één zijde en één hoek weet, zou je een andere zijde kunnen berekenen. Hieronder een voorbeeld.

In driehoek PQR is hoek P bekend en zijde QR. We willen zijde PR en PQ gaan berekenen.

We beginnen met zijde PQ. Vanuit hoek P weten we de overstaande rechthoekszijde (QR) en willen we de aanliggende rechthoekszijde gaan berekenen. Bij de overstaande en aanliggende zijde gebruiken we de tangens.

Zo kan je ook de schuine zijde PR gaan berekenen. Je weet de overstaande zijde vanuit hoek P en je wilt de schuine weten. SOS CAS TOA laat dan zien dat je bij overstaand en schuin de sinus mag gebruiken (SOS).

Video

Wil je meer weten over het rekenen met SOS CAS en TOA? Kijk dan onderstaande video van WiskundeAcademie.