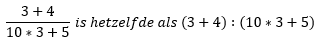Rekenen met breuken

Breuken zul je vast wel herkennen. Zelfs op de basisschool heb je hier al kennis mee gemaakt. Ken je de opdrachten nog? Bijvoorbeeld "Jantje viert zijn kinderfeestje met zes andere kinderen en hij wil iedereen een stukje taart geven dat even groot is: hoeveelste deel van de taart krijgt iedereen?" Maar na de basisschool ontdek je dat breuken heel wat moeilijker kunnen zijn dan 1/7e deel van een taart. Daarom leggen we je in dit artikel van alles uit over breuken en hoe je daarmee rekent.

Wat is een breuk?

Een breuk is eigenlijk een andere manier om ‘delen door’ weer te geven. Je deelt getal A door getal B en dat levert de volgende breuk op: A/B. Dit komt je vast bekend voor. Denk maar aan alle opdrachten die je vroeger hebt gemaakt over taarten in stukjes snijden. Als je een kwart van de taart pakt, dan pak je 1 van de 4 stukjes en dan heb je 1/4 van de taart. Een breuk geeft eigenlijk een verhouding weer. Bij een taart is dat de verhouding tussen het deel dat jij pakt en het geheel: deel/geheel. Het getal boven de deelstreep noemen we de teller en het getal onder de deelstreep de noemer.

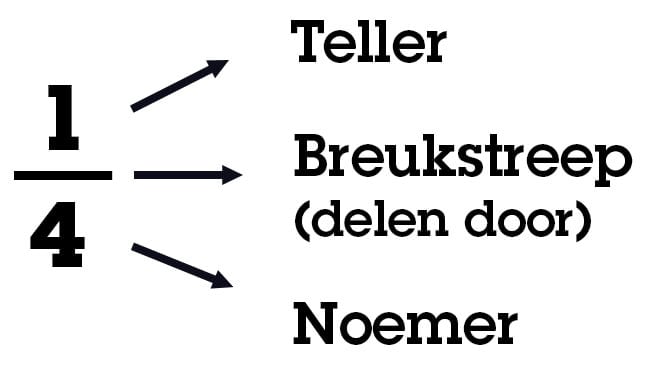
Waarom schrijven we dan niet gewoon ‘gedeeld door’? Omdat breuken gecompliceerde berekeningen een stuk overzichtelijker maken. Als je met grote combinaties van getallen boven en onder de deelstreep werkt, zijn breuken duidelijker. Je hoeft dan niet steeds 'gedeeld door' op te schrijven, maar kun je het gewoon makkelijk aflezen uit de formule.

Hoe gebruik je breuken?

Bij een breuk bereken je eerst alles boven de deelstreep, vervolgens alles onder de deelstreep en dáárna deel je het pas door elkaar. Als geheugensteuntje kun je doen alsof alles zowel boven als onder de deelstreep tussen haakjes staat.

Voorbeeld

Als je een breuk tegenkomt, wil je die zo ver mogelijk vereenvoudigen. Dit betekent dat je de getallen boven en onder de deelstreep verandert in zo klein mogelijke hele getallen. Hoe versimpel je zo’n breuk dan precies? Je deelt de teller en de noemer steeds door hetzelfde getal. Dat betekent dus dat de teller en noemer allebei deelbaar moeten zijn door datzelfde getal. Als er geen getal meer is waar de teller en noemer allebei door gedeeld kunnen worden, dan is de breuk versimpeld. Het versimpelen mag in stapjes. Je hoeft het niet in één keer te zien.

Voorbeeld

Want 7 is deelbaar door 7 en 35 is ook deelbaar door 7.

Wat zijn de rekenregels bij breuken?

Bij breuken komen er een aantal rekenregels om de hoek kijken. Welke rekenregels je precies gebruikt, hangt af van wat je met de breuk doet. Hieronder leggen dit in meer detail uit.

Breuken optellen en aftrekken

Voordat je breuken mag optellen en aftrekken, moeten de breuken aan één eis voldoen: ze moeten dezelfde noemer hebben. Als dat al het geval is, dan mag je de tellers bij elkaar optellen of aftrekken om er één breuk van te maken. Dit wordt duidelijk in deze rekenregel:

Als de noemers niet aan elkaar gelijk zijn, moet je ze gelijk maken. Je kunt dat doen door ze met elkaar te vermenigvuldigen. Als je de noemer met iets vermenigvuldigt, moet je de teller met datzelfde vermenigvuldigen zodat de verhouding gelijk blijft. Je vermenigvuldigt de hele breuk als het ware met 1, namelijk met D/D = 1.

Let op: Een getal kan altijd geschreven worden als een breuk met 1 als noemer. Dit mag omdat alles gedeeld door 1 zichzelf is. Kijk maar: 5 = 5/1. Er verandert dus niets tussen A = A/1. Door een gewoon getal als een breuk te schrijven, kun je die soms makkelijker gebruiken bij rekenregels. Bij optellen gaat dat als volgt:

Breuken vermenigvuldigen

Om breuken te vermenigvuldigen met elkaar, moet je simpelweg de tellers vermenigvuldigen en de noemers vermenigvuldigen. Dat zijn je nieuwe teller en noemer en dat ziet er als volgt uit:

Met een gewoon getal in plaats van een breuk zou de regel er als volgt uitzien:

Video

Wil je meer weten over het vermenigvuldigen van breuken? Bekijk dan deze video van WiskundeAcademie:

Breuken delen

Om breuken door elkaar te delen moet je het volgende onthouden: 'delen door' is hetzelfde als vermenigvuldigen met het omgekeerde. Dit is logisch als je bedenkt dat de acties ‘delen door’ en ‘vermenigvuldigen’ ook eigenlijk elkaars tegenovergestelde zijn. Onthoud deze regel goed! Het houdt in dat je de breuk in de noemer vermenigvuldigt met de omgekeerde breuk uit de teller. Hieronder staat de regel nog een keer uitgeschreven.

Met een gewoon getal in plaats van een breuk zou de regel er als volgt uitzien:

Of

Video

Wil je meer uitleg over het delen van breuken? Dan is deze video van WiskundeAcademie handig:

Breuken gelijkstellen

Als je aan beide kanten van een =-teken een breuk hebt staan, dan stel je die breuken dus aan elkaar gelijk. Voor die situatie is ook een handige rekenregel.

In deze situatie mag je de tellers en noemers dus kruislings vermenigvuldigen. Je vermenigvuldigt de teller van de ene breuk met de noemer van de andere breuk. Wat we eigenlijk doen is de breuk wegwerken door deze te vermenigvuldigen met zijn noemer. Maar wat we aan de ene kant van het =-teken doen, moeten we ook aan de andere kant van het =-teken doen. Daarom vermenigvuldigen we beide breuken met beide noemers, zoals hieronder nog eens uitgeschreven.

Als een van de twee breuken een gewoon getal is, kan je dat weer zien als .

Breuken in wortels

Het kan ook voorkomen dat een breuk onder een wortelteken staat of dat er een wortelteken in de breuk staat.

Let op: Als de gehele breuk onder een wortelteken staat, mag je dat ook schrijven als een wortel boven en een wortel beneden. Soms helpt dat met versimpelen.