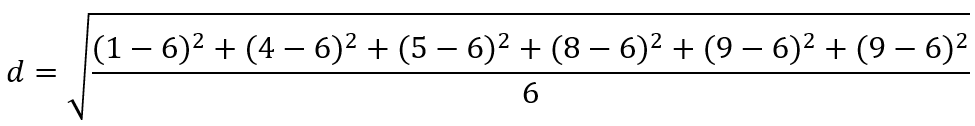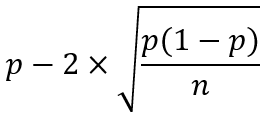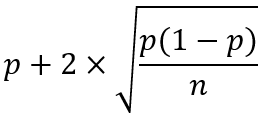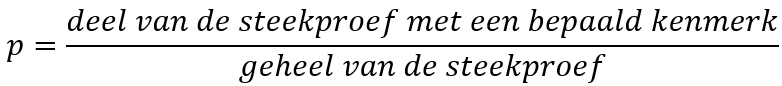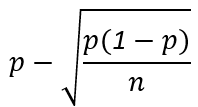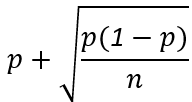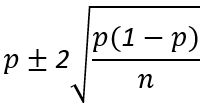Normale verdeling
Als je een aantal willekeurige volwassen Nederlanders op een rijtje zet, zal het grootste deel van deze personen een lengte hebben tussen de 160 cm en 190 cm. Slechts een klein deel zal groter zijn dan 190 cm of kleiner dan 160 cm. De lengtes van deze mensen is op een bepaalde manier verdeeld. Een verdeling die vaak voorkomt in het dagelijks leven, is de normale verdeling. In dit artikel leggen we je daarom alles uit over de normale verdeling!
Wat is de normale verdeling?

De normale verdeling is een verdeling van gegevens die verloopt volgens een frequentiepolygoon met de vorm van een kerstklok. Deze verdeling komt vaak voor en wordt daarom de normale verdeling genoemd. Het beschrijft hoe data zich verspreid in de wereld van statistiek.
De normale verdeling heeft vijf handige eigenschappen die vaak worden gebruikt:
- De normale verdeling is altijd in de vorm van een kerstklok.
- Het gemiddelde ligt altijd in het midden, op de hoogste piek.
- De mediaan ligt altijd in het midden, op de hoogste piek.
- De modus ligt altijd in het midden, op de hoogste piek.
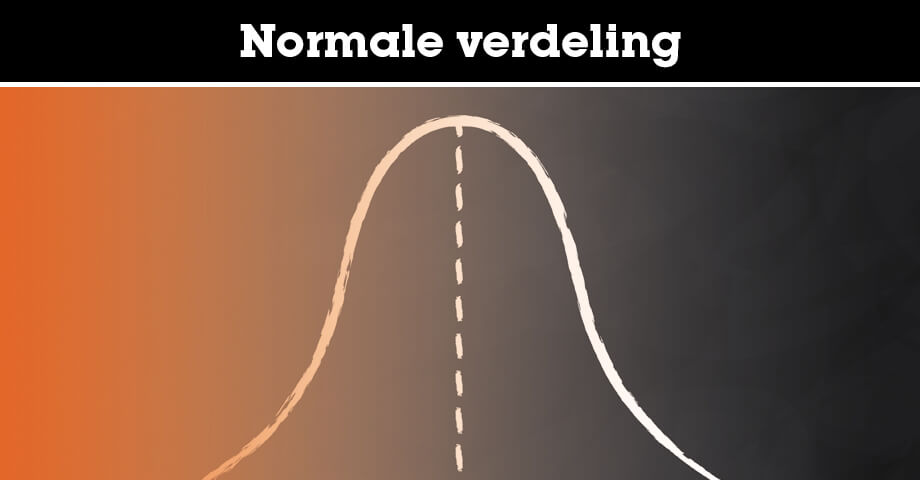
- Het buigpunt ligt precies 1 standaardafwijking van het gemiddelde af.
In de afbeelding hieronder zie je een voorbeeld van hoe een normale verdeling eruit ziet:
Wat is de standaardafwijking?

De standaardafwijking geeft de spreiding van verschillende getallen in een waarneming weer. De standaardafwijking wordt gebruikt om de verdeling van een normale verdeling te geven. Niet alle gegevens zullen namelijk precies op het gemiddelde liggen. De gegevens wijken (bijna) altijd af en om die afwijking simpel te maken, noemen we het de standaardafwijking of de standaarddeviatie.
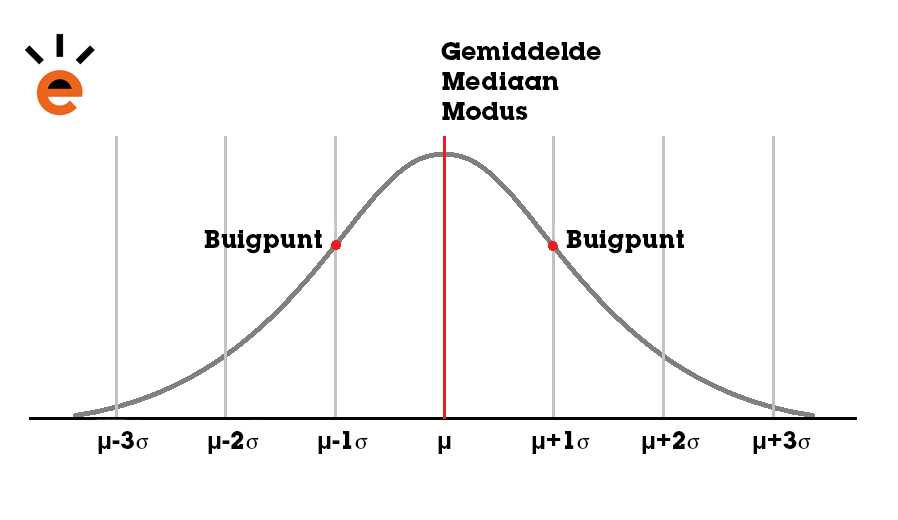
Vaak wordt de standaardafwijking gegeven in een opdracht, maar je kunt hem ook zelf berekenen als je alle gegevens kent. Om de standaardafwijking te berekenen, wordt de volgende formule gebruikt:
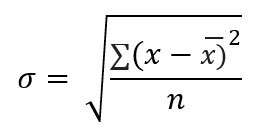
Om deze formule toe te passen, dienen eerst alle afwijkingen te worden berekend. Daarna kun je de standaardafwijking berekenen.
- De formule voor een afwijking:
Hierbij is:- d de afwijking
- x ieder getal
het gemiddelde
- Wanneer alle afwijkingen zijn berekend, worden ze allemaal gekwadrateerd en bij elkaar opgeteld.
- Daarna wordt dit gedeeld door het aantal afwijkingen n.
- Tot slot wordt hiervan de wortel genomen.
In de formule wordt het sommatieteken ∑ gebruikt, maar eigenlijk worden alle afwijkingen los berekend, gekwadrateerd en opgeteld.
Voorbeeld:
Stel, je krijgt de volgende getallen: 1, 4, 5, 8, 9 en 9.
Allereerst is het gemiddelde benodigd. Deze is namelijk later ook nodig om de afwijkingen uit te rekenen. Het gemiddelde is:
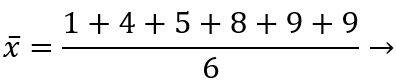
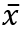
Wanneer de formule wordt ingevuld, dien je rekening te houden met het sommatieteken ∑.
Dit geeft een standaardafwijking van d = 2,943...
Het afronden van dit getal geeft een standaardafwijking van ≈ 2,9
Zijn er vuistregels voor de normale verdeling?
Er zijn twee parameters of vuistregels die bepalen hoe de normale verdeling eruit komt te zien:
- Het gemiddelde μ (mu).
- De standaardafwijking σ (sigma).
De meeste waarden liggen rond het gemiddelde en daardoor op de hoogste piek. Hoe verder je van het gemiddelde afgaat, des te minder waarden er zullen zijn. De afstand tot het gemiddelde wordt aangegeven met standaardafwijkingen. Hoe hoog die standaardafwijking precies is, kan per situatie verschillen.
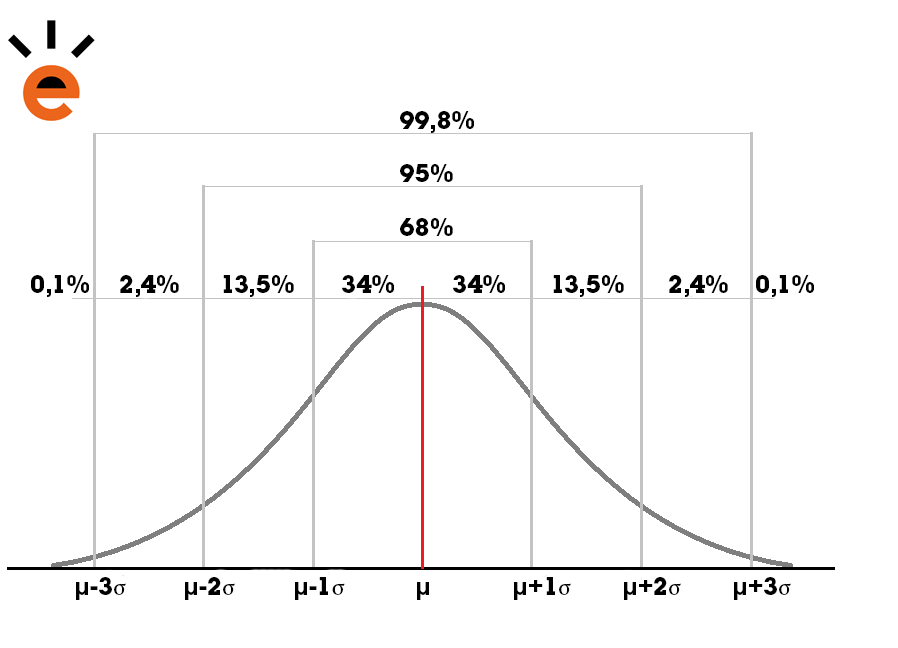
Per standaardafwijking van het gemiddelde ziet dat er als volgt uit:
- 1 standaardafwijking van het gemiddelde, bevat 68% van alle data.
- 2 standaardafwijkingen van het gemiddelde, bevat 95% van alle data.
- 3 standaardafwijkingen van het gemiddelde, bevat 99,8% van alle data.
Met '1 standaardafwijking van het gemiddelde' wordt hier de ruimte bedoeld tussen 'het gemiddelde + 1 standaardafwijking' en'het gemiddelde - 1 standaardafwijking'.
Let op: 3 standaardafwijkingen vanaf het gemiddelde bevat niet alle waarden. Dit heeft als reden dat er enkele uitschieters zijn die veel groter of kleiner zijn dan de rest van de waarden.
Voorbeeld:
Stel dat een klas het wiskundecijfer terugkrijgt. Alle scores zijn normaal verdeeld met een gemiddeld cijfer van 6,0 en een standaardafwijking van 1,5. De kans dat iemand een 4,5 heeft is dus even groot als de kans dat iemand een 7,5 heeft.
- 68% van de klas zal een cijfer tussen de 4,5 en 7,5 hebben.
- 95% van de klas zal een cijfer tussen de 3 en 9 hebben.
- 99,8% van de klas zal een cijfer tussen de 1,5 en 10,5 hebben.
Een 10,5? Hoe is dat mogelijk? De cijfers hoeven natuurlijk niet echt op 10,5 te zitten, maar de grens van het 99,8%-gebied ligt in dit voorbeeld simpelweg op 10,5. In werkelijkheid houden de cijfers natuurlijk gewoon op bij maximaal 10.
Wat is het betrouwbaarheidsinterval?
Het betrouwbaarheidsinterval is een maatstaf om te zien hoe betrouwbaar een onderzoek is. In de wiskunde zijn er verschillende intervallen, waaronder het 95% betrouwbaarheidsinterval en het 68% betrouwbaarheidsinterval voor de populatieproportie.
Het 95% betrouwbaarheidsinterval wil zeggen dat er 95 onderzoeken een correcte uitkomst moeten hebben als er 100 onderzoeken worden uitgevoerd. Het geeft antwoord op de vraag: "Tussen welke twee waarden/grenzen ligt 95% van de gegevens?". Dit valt te berekenen met de volgende formules:
- Linker grens van het 95% betrouwbaarheidsinterval:
- Rechter grens van het 95% betrouwbaarheidsinterval:
Het 95% betrouwbaarheidsinterval geeft 2 grenzen aan. Daarom wordt het 95% betrouwbaarheidsinterval 2 keer berekend.
Hierbij is:
- n de steekproefomvang
- p de steekproefproportie (getal tussen 0 en 1)
De steekproefproportie wordt met de volgende formule berekend:
Let op: de steekproefproportie wordt gebruikt om het 95% betrouwbaarheidsinterval voor de populatieproportie te berekenen.
Een ander betrouwbaarheidsinterval is het 68% betrouwbaarheidsinterval, welke wordt berekend door middel van de volgende formules:
- Linker grens van het 68% betrouwbaarheidsinterval:
- Rechter grens van het 68% betrouwbaarheidsinterval:
Voorbeeld:
Er is een onderzoek gedaan naar alle scholieren van een school met een bijbaantje. Uit een aselecte steekproef van 3260 leerlingen blijkt dat 1530 scholieren een bijbaantje hebben. Bereken het 95%-betrouwbaarheidsinterval voor de steekproefproportie scholieren met een bijbaantje. Geef je antwoord in 2 decimalen.
Er wordt hier gevraagd naar het 95%-betrouwbaarheidsinterval. Dat betekent dat er 2 antwoorden benodigd zijn: 1 voor elke grens. Allereerst nemen we de formule voor het 95%-betrouwbaarheidsinterval:
Om deze formule in te vullen, zal eerst de steekproefproportie moeten worden berekenend:
Invullen geeft:
Het 95%-betrouwbaarheidsinterval is [0,45 ; 0,49]. Met andere woorden: je kunt met 95% zekerheid zeggen dat het percentage scholieren dat een bijbaantje heeft, tussen de 45% en 49% ligt.
Let op! Er wordt gesproken over het 95%-betrouwbaarheidsinterval, daarom dient het antwoord ook als interval te worden genoteerd.
Hoe reken je met de normale verdeling op een grafische rekenmachine?
Om de normale verdeling te plotten op de grafische rekenmachine, is het belangrijk om te weten welke rekenmachine er wordt gebruikt:
TI-84 Plus CE-T
Bij de TI-84 Plus CE-T kies je voor 2nd → VARS om bij het DISTR-menu te komen. Vervolgens kies je voor invNorm en kan de gegeven of berekende waarde worden ingevuld. Dit zal een normale verdeling plotten, maar kan ook een links-scheve of rechts-scheve verdeling maken.
CASIO FX-CG50
Bij de CASIO FX-CG50 kies je voor het statistiek menu en druk op de toets F5 (DISTR) om naar het DISTR-menu te gaan. Druk daarna op toets F1 (NORM) om met de normale verdeling te rekenen.
Er ontstaan twee belangrijke opties:
- NCD: de Normale Cumulatieve Distributie wordt gebruikt om de kans tussen twee grenzen te berekenen bij een normale verdeling. Cumulatief staat voor een percentage, daardoor zal het hoogstwaarschijnlijk een percentageverschil zijn. Bijv.: 68% als je de kans op een gebied tussen 1 standaardafwijking wilt berekenen.
- InvN: de Inverterende Normale wordt gebruikt om de waarde van een grens te berekenen. Met andere woorden: op welke hoogte bevindt deze grens zich?
Kies de juiste soort die het beste past en vul de gekregen of berekende waarden in op de grafische rekenmachine.
Video
Wil je meer weten over de normale verdeling en de betrouwbaarheidsintervallen? Kijk dan onderstaande video van Math with Menno!